在计算机科学中,有一个专门的分支研究问题的可计算性,叫做计算理论。
我们用计算机算法来解决一个问题,如果一个问题被证明很难计算,或者只能暴力枚举来解决,那么我们就不必花大力气去质疑使用的算法是不是错了,为什么这么慢,计算怎么久都没出结果,到底有没有更好的算法。
计算机科学把一个待解决的问题分类为:P 问题,NP 问题,NPC 问题,NP-hard 问题。
一、P 和 NP 问题
类似于 O(1),O(logn),O(n) 等复杂度,规模 n 出现在底数的位置,计算机能在多项式时间解决,我们称为多项式级的复杂。
类似于 O(n!),O(2^n) 等复杂度,规模 n 出现在顶部的位置,计算机能在非多项式时间解决,我们称为非多项式级的复杂度。
如果一个问题,可以用一个算法在多项式时间内解决,它称为 P 问题(P 为 Polynominal 的缩写,多项式)。
比如求1加到100的总和,它的时间复杂度是 O(n),是多项式时间。
然而有些问题,只能用枚举的方式求解,时间复杂度是指数级别,非多项式时间,但是只要有一个解,我们能在多项式时间验证这个解是对的,这类问题称为 NP 问题。
也就是说,如果我们只能靠猜出问题的一个解,然后可以用多项式时间来验证这个解,这些问题都是 NP 问题。
所以,按照定义,所有的 P 问题都是 NP 问题。
计算理论延伸出了图灵机理论,自动机=算法。
有两种自动机,一种是确定性自动机,机器从一个状态到另外一个状态的变化,只有一个分支可以走,而非确定性自动机,从一个状态到另外一个状态,有多个分支可以走。P 问题都可以用两种机器来解决,当非确定性自动机退化就变成了确定性自动机,而 NP 问题只能用非确定性自动机来解决。
自动机对 N 和 NP 问题的定义:
可以在确定性自动机以多项式时间解决的问题,称为 P 问题,可以在多项式时间验证答案的问题称为 NP 问题。而 NP 问题是可以在非确定型自动机以多项式时间解决的问题(NP 两字为 Non-deterministicPolynomial 的缩写,非确定多项式)。
数学,计算机科学,哲学,三个学科其实交融在一起,自动机是一台假想的机器,世界其实也可以认为是一个假想的机器,所以世界可以等于一台自动机吗,大家可以发挥想象力,在以后的日子里慢慢体会,建议购买书籍《计算理论》补习相关知识。
二、NPC 和 NP-hard 问题
存在这样一个 NP 问题,所有的 NP 问题都可以约化成它。换句话说,只要解决了这个问题,那么所有的 NP 问题都解决了。其定义要满足2个条件:
- 它得是一个
NP问题。 - 所有的
NP问题都可以约化到它。
这种问题称为 NP 完全问题(NPC)。按照这种定义,NP 问题要比 NPC 问题的范围广。
那什么是 NP-hard 问题,其定义要满足2个条件:
- 所有的
NP问题都可以约化到它。 - 它不是一个
NP问题。
也就是说,NP-hard 问题更难,你只要解决了 NP-hard 问题,那么所有的 NP 问题都可以解决。但是,这个问题本身不是一个 NP 问题,也就是解不能在多项式时间内被验证。
比如你有一个交际网,每个人是一个节点,认识的人之间相连。你要通过一个最快、最省钱、最能提升你个人形象、最没有威胁、最不影响你日常生活的方式认识一个萌妹,你怎么证明你认识这个萌妹是最省钱的呢?-来自知乎回答。
我们一旦发现一个问题是 NPC 问题,那么我们很难去准确求出其解,只能暴力枚举,靠猜。
三、总结
各类问题可以用这个图来表示:
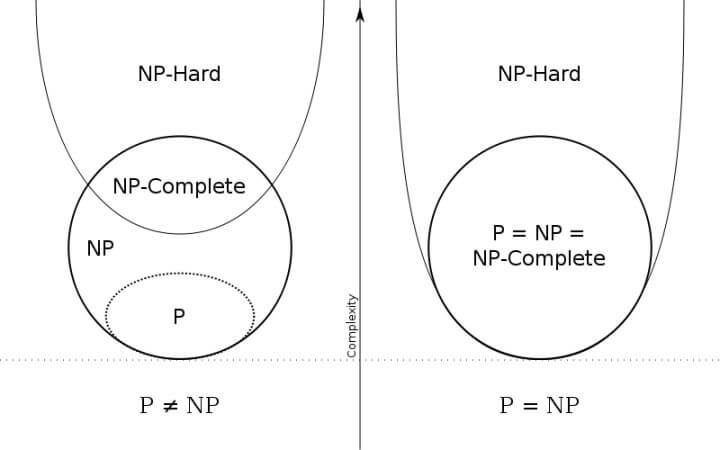
“P=NP“ 问题的目标,就是想要知道 P 和 NP 这两个集合是否相等。为了证明两个集合( A 和 B)相等,一般都要证明两个方向:
A包含B。B包含A。
我们已经说过 NP 包含了 P。因为任何一个非确定性机器,都能被当成一个确定性的机器来用。你只要不使用它的“超能力”,在每个分支点只探索一条路径就行。
所以 “P=NP“ 就在于 P 是否也包含了 NP。也就是说,如果只使用确定性计算机,能否在多项式时间之内,解决所有非确定性计算机能在多项式时间内解决的问题。
