108_convert_sorted_array_to_binary_search_tree

108. 将有序数组转换为二叉搜索树 简单

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：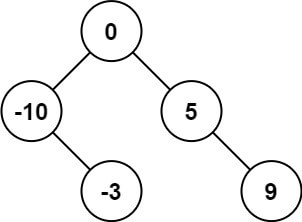

示例 2：

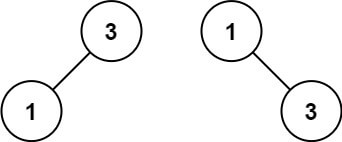
输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 按 严格递增 顺序排列

代码参考：

package main

import "fmt"

func main() {
    root := sortedArrayToBST([]int{0, 1, 2, 3, 4, 5})
    fmt.Println(root)
    fmt.Println(root.Left)
    fmt.Println(root.Left.Left)
    fmt.Println(root.Left.Right)
    fmt.Println(root.Right)
    fmt.Println(root.Right.Left) // bingo
}

func sortedArrayToBST(nums []int) *TreeNode {
    return construct(nums)
}

func construct(nums []int) *TreeNode {
    n := len(nums)
    if n == 0 {
        return nil
    }
    if n == 1 {
        return &TreeNode{Val: nums[0]}
    }

    // 尽可能地取中间的值作为根节点
    mid := n / 2
    root := &TreeNode{Val: nums[mid]}
    root.Left = construct(nums[:mid])    // 左子数组作为左子树
    root.Right = construct(nums[mid+1:]) // 右子数组作为右子树 // 地达到 AVL 树特点
    return root
}