897_increasing_order_search_tree

897. 递增顺序搜索树 简单

给你一棵二叉搜索树，请你 按中序遍历 将其重新排列为一棵递增顺序搜索树，使树中最左边的节点成为树的根节点，并且每个节点没有左子节点，只有一个右子节点。

示例 1：

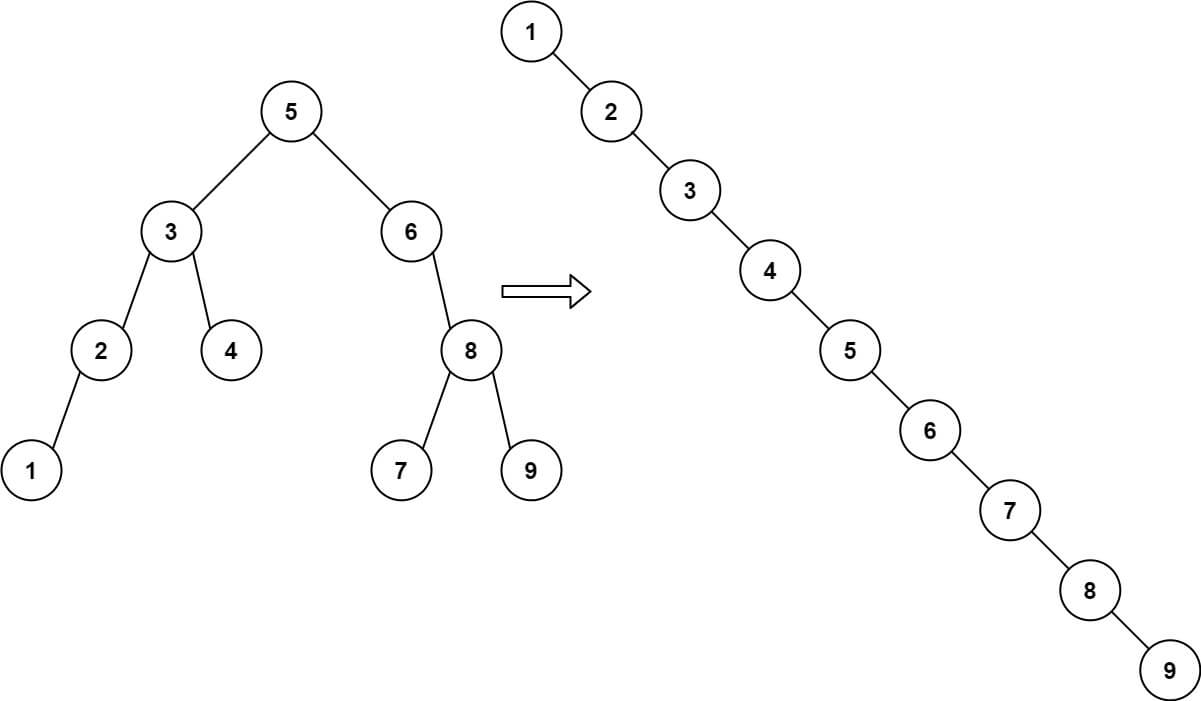
输入：root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
输出：[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

示例 2：

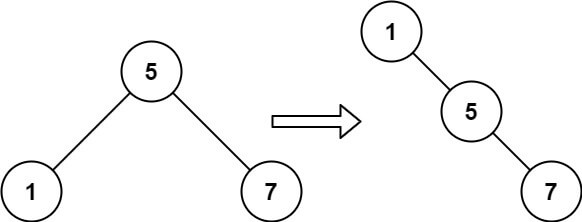
输入：root = [5,1,7]
输出：[1,null,5,null,7]

提示：

• 树中节点数的取值范围是 [1, 100]
• 0 <= Node.val <= 1000

代码参考：

package main

import "fmt"

func main() {
    root := &TreeNode{Val: 1}
    root.Left = &TreeNode{Val: 0}
    fmt.Println(increasingBST(root)) // 0 bingo
}

// 可以先递归中序遍历把数记在数组，再重建右斜树
// 不过用 stack 可以一边遍历一边建树
func increasingBST(root *TreeNode) *TreeNode {
    if root == nil {
        return nil
    }

    var newRoot *TreeNode
    var newCur *TreeNode

    var stack []*TreeNode
    cur := root
    for cur != nil || len(stack) > 0 {
        // 先走到最左节点记下新头节点
        if cur != nil {
            stack = append(stack, cur)
            cur = cur.Left
            continue
        }

        if newRoot == nil {
            newRoot = stack[len(stack)-1] // leftest
            newCur = newRoot
        } else {
            newCur.Right = stack[len(stack)-1]
            newCur = newCur.Right
        }
        stack = stack[:len(stack)-1] // pop
        newCur.Left = nil            // 把原节点的左子树给砍掉
        cur = newCur.Right           // 中序遍历
    }

    newCur.Right = nil // bingo
    return newRoot
}